版本：0.12.0

InferBound Pass

InferBound pass 在 normalize 之后、ScheduleOps build_module.py 之前运行。InferBound 的主要工作是创建 bounds map，为程序中的每个 IterVar 指定一个 Range。接下来这些 bounds 会传递给 ScheduleOps，用于设置 For 循环的范围，参阅 MakeLoopNest，以及设置分配缓冲区的大小（BuildRealize）以及其他用途。

InferBound 的输出是从 IterVar 到 Range 的映射：

Map<IterVar, Range> InferBound(const Schedule& sch);

回顾 Range 和 IterVar 类：

namespace HalideIR {
namespace IR {
     class RangeNode : public Node {
     public:
             Expr min;
             Expr extent;
             // 剩余部分省略
     };
     }}

namespace tvm {
     class IterVarNode : public Node {
     public:
             Range dom;
             Var var;
             // 剩余部分省略
     };
}

注意，IterVarNode 还包含一个 Range dom。这个 dom 的值是否有意义，取决于 IterVar 的创建时间。例如，调用 tvm.compute 时，会为每个 axis 和 reduce axis 创建一个 IterVar ，其中 dom 等于调用 tvm.compute 时提供的 shape。

另一方面，调用 tvm.split 时，会为内轴和外轴创建 IterVars，但这些 IterVars 没有被赋予有意义的 dom 值。

在任何情况下，IterVar 的 dom 成员在 InferBound 期间都不会被修改。但 IterVar 的 dom 成员有时用作 Range InferBound 计算的默认值。

为了理解 InferBound pass，我们先来看一下 TVM 代码库概念。

InferBound 接收一个参数，即 Schedule。这个 schedule 对象及其成员包含正在编译的程序的所有信息。

TVM schedule 由 stage 组成。每个 stage 只有一个 Operation，例如 ComputeOp 或 TensorComputeOp。每个 Operation 都有一个 root_iter_vars 列表，在 ComputeOp 的情况下，它由 axis IterVar 和 reduce axis IterVar 组成。

每个 Operation 还包含许多其他 IterVar，它们通过 Operation 的 IterVarRelations 列表相关联。每个 IterVarRelation 代表 schedule 中的 split、fuse 或 rebase。例如，在 split 的情况下，IterVarRelation 指定被拆分的父级 IterVar，以及两个子级 IterVar：内部和外部。

namespace tvm {
     class ScheduleNode : public Node {
     public:
             Array<Operation> outputs;
             Array<Stage> stages;
             Map<Operation, Stage> stage_map;
             // 剩余部分省略
     };

     class StageNode : public Node {
     public:
             Operation op;
             Operation origin_op;
             Array<IterVar> all_iter_vars;
             Array<IterVar> leaf_iter_vars;
             Array<IterVarRelation> relations;
             // 剩余部分省略
     };

     class OperationNode : public Node {
     public:
             virtual Array<IterVar> root_iter_vars();
             virtual Array<Tensor> InputTensors();
             // 剩余部分省略
     };

     class ComputeOpNode : public OperationNode {
     public:
             Array<IterVar> axis;
             Array<IterVar> reduce_axis;
             Array<Expr> body;
             Array<IterVar> root_iter_vars();
             // 剩余部分省略
     };
}

在 TVM 的 context 中，张量表示操作的输出。

class TensorNode : public Node {
public:
     // 源操作，可以是 None
     // 这个 Tensor 是这个 op 输出的
     Operation op;
     // 源操作的输出索引
     int value_index;
};

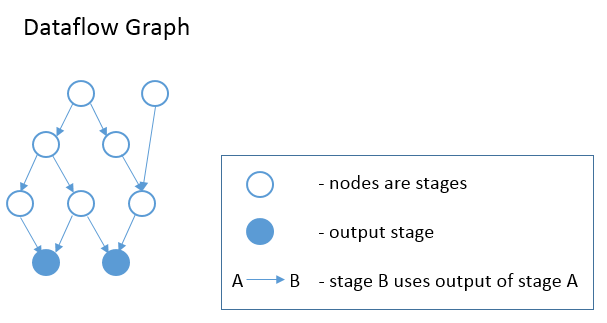
上面的 Operation 类声明中，可以看到每个 operation 还有一个 InputTensor 列表。因此，schedule 的各个 stage 形成了一个 DAG，其中每个 stage 都是图中的一个节点。若 Stage B 的 operation 有一个输入张量，其源操作是 Stage A 的 op，那么图中从 Stage A 到 Stage B 有一个 edge。简而言之，若 B 消耗了一个由 A 产生的张量，则从 A 到 B 会出现一个 edge。参见下图。这个计算图是在 InferBound 开始时调用 CreateReadGraph 创建的。

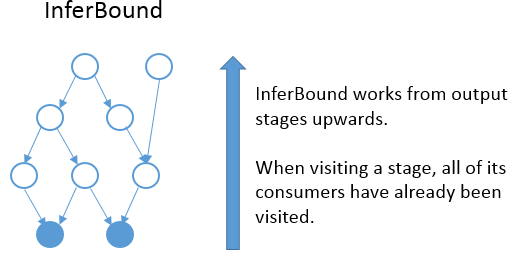
InferBound 使 pass 遍历计算图，每个 stage 访问一次。InferBound 从输出 stage 开始（即上图中的实心蓝色节点），然后向上移动（在边缘的相反方向上）。这是通过对计算图的节点执行反向拓扑排序来实现的。因此，当 InferBound 访问一个 stage 时，它的每个 consumer stage 都已经被访问过。

InferBound pass 如以下伪代码所示：

Map<IterVar, Range> InferBound(const Schedule& sch) {
     Array<Operation> outputs = sch->get_outputs();
     G = CreateGraph(outputs);
     stage_list = sch->reverse_topological_sort(G);
     Map<IterVar, Range> rmap;
     for (Stage s in stage_list) {
             InferRootBound(s, &rmap);
             PassDownDomain(s, &rmap);
     }
     return rmap;
}

InferBound pass 有两个不是很明显的属性：

InferBound 访问一个 stage 后，stage 中所有 IterVar 的范围都会在 rmap 中设置。
每个 IterVar 的 Range 只在 rmap 中设置一次后就不会再变了。

因此，仍然需要解释 InferBound 在访问 stage 时的主要作用。从上面的伪代码中可以看出，InferBound 在每个 stage 调用了两个函数：InferRootBound 和 PassDownDomain。InferRootBound 的目的是设置 stage 每个 root_iter_var 的 Range（在 rmap 中）。（注意：InferRootBound 不设置任何其他 IterVar 的 Range，只设置属于 root_iter_vars 的那些）。PassDownDomain 的目的是将此信息传播到 stage 的其余 IterVars。当 PassDownDomain 返回时，stage 的所有 IterVars 在 rmap 中都有已知的 Range。

文档的其余部分将深入探讨 InferRootBound 和 PassDownDomain 的详细信息。由于 PassDownDomain 描述起来更简单，因此首先介绍它。

IterVar Hyper-graph

如上所述，InferBound pass 遍历 stage 计算图。但是，在每个 stage 中都有另一个节点为 IterVars 的计算图。 InferRootBound 和 PassDownDomain 在这些 IterVar 计算图上传递消息。

回想一下，stage 的所有 IterVar 都由 IterVarRelations 关联。一个 stage 的 IterVarRelations 构成一个有向无环 hyper-graph，计算图中每个节点对应一个 IterVar，每条 hyper-edge 对应一个 IterVarRelation。也可以将这个 hyper-graph 表示为 DAG，如下图所示更易于可视化。

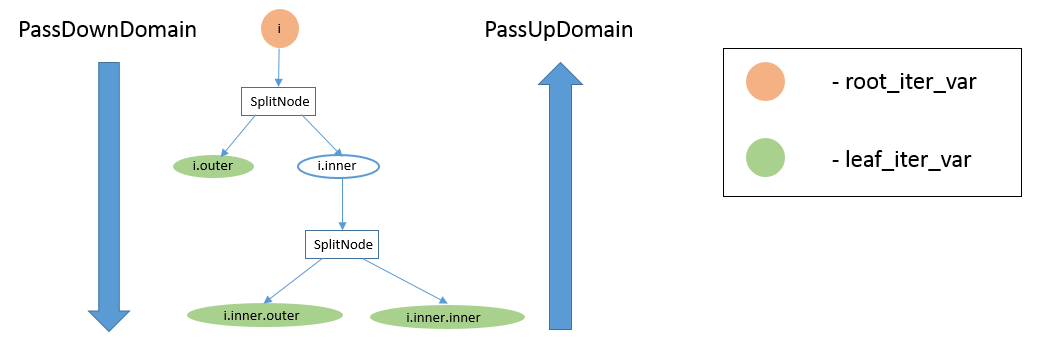
上图显示了一个 stage 的 IterVar hyper-graph。该 stage 有一个 root_iter_var i，它已被拆分，生成的内轴 i.inner 已再次拆分。该 stage 的 leaf_iter_vars 为绿色图示：i.outer、i.inner.outer 和 i.inner.inner。

消息传递函数被命名为「PassUp」或「PassDown」，取决于消息是从 DAG 中的子代传递给其父代（「PassUp」），还是从父代传递给其子代（「PassDown」）。例如，上图左侧的大箭头显示 PassDownDomain 从根 IterVar i 向其子 i.outer 和 i.inner 发送消息。

PassDownDomain

PassDownDomain 的作用是为 root_iter_vars 取 InferRootBound 产生的 Range，并设置 stage 中所有其他 IterVars 的 Range。

PassDownDomain 遍历 stage 的 IterVarRelations。IterVarRelation 有三种可能的类型：split、fuse 和 rebase。最有趣的案例（因为它还有改进空间）是表示 split 的 IterVarRelations。

根据父级 IterVar 的已知 Range，来设置 split 的内部 IterVar 和外部 IterVar 的 Range，如下：

rmap[split->inner] = Range::FromMinExtent(0, split->factor)
rmap[split->outer] = Range::FromMinExtent(0, DivCeil(rmap[split->parent]->extent, split->factor))

当 split->factor 没有平均划分父节点的范围时，就有机会收紧 InferBound 产生的边界。假设 parent 的范围是 20，split 因子是 16。那么在外部循环的第二次迭代中，内部循环只需要进行 4 次迭代，而非 16 次。如果 PassDownDomain 可以设置 split->inner 的范围为 min (split->factor, rmap[split->parent]->extent - (split->outer * split->factor))，则内部变量的范围将根据正在执行的外部循环的迭代进行适当调整。

对于 Fuse 关系，根据已知的内外 IterVar 的 Range 设置 fuse 后的 IterVar 的 Range，如下：

rmap[fuse->fused] = Range::FromMinExtent(0, rmap[fuse->outer]->extent * rmap[fuse->inner]->extent)

InferRootBound

InferBound 调用 InferRootBound，然后在 stage 计算图中的每个 stage 调用 PassDownDomain。InferRootBound 的目的是设置 Stage 操作的每个 root_iter_var 的 Range。这些 Range 会用 PassDownDomain 传到 Stage 的其余 IterVars。注意，InferRootBound 不会设置任何其他 IterVar 的 Range，仅设置属于 Stage 的 root_iter_vars 的那些。

若 Stage 是输出 Stage 或占位符，InferRootBound 只需将 root_iter_var Range 设置为其默认值。root_iter_var 的默认 Range 取自 IterVar 的 dom 成员（参阅上面的 IterVarNode 类声明）。

否则，InferRootBound 将遍历 stage 的 consumer。为每个 consumer 的 IterVar 创建 IntSet，如下所示。

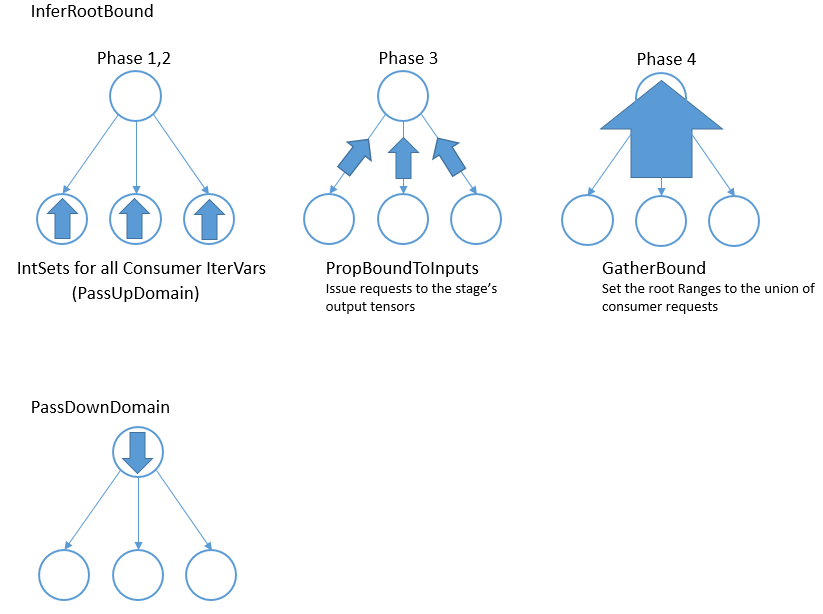
阶段 1）IntSet 为 consumer 的 leaf_iter_vars 初始化，并通过 PassUpDomain 传到 consumer 的 root_iter_vars（阶段 2）。这些 IntSet 用于创建 consumer stage（阶段 3）的输入张量的 TensorDom。最后，一旦所有 consumer 都处理完毕，InferRootBound 调用 GatherBound，根据 TensorDoms（阶段 4）设置 stage 的 root_iter_vars 的 Range。

这个过程看起来很复杂。原因之一是一个 stage 可以有多个 consumer。每个 consumer 都有不同的要求，且必须以某种方式整合。类似地，该 stage 可能会输出多个张量，并且每个 consumer 只使用这些张量的特定子集。此外，即使 consumer 使用特定的张量，它也可能不会使用张量的所有元素。

如上所述，consumer 可能只需要每个张量中的少量元素。consumer 可以看成是针对输出张量某些区域，向 stage 发出的请求。阶段 1-3 的工作是建立每个 consumer 所需的每个输出张量的区域。

IntSet

在 InferRootBound 期间，Range 被转换为 IntSet，并且在 IntSet 上执行消息传递。因此，了解 Range 和 IntSet 之间的区别很重要。「IntSet」这个名称表明它可以表示任意整数集，例如 A = 13。这肯定比 Range 更具表现力，Range 只表示一组连续的整数，例如 B = 12。

然而，目前 IntSet 只有三种类型：IntervalSets、StrideSets 和 ModularSets。与 Range 类似，IntervalSets 仅表示连续整数的集合。StrideSet 由基本 IntervalSet、步长列表和范围列表定义。StrideSet 未被使用，ModularSet 只用于前端。

因此，目前在 TVM 中并非所有的整数集合都可以用 IntSet 来表示。例如，上例中的集合 A 不能用 IntSet 表示。将来 IntSet 的功能可以扩展为处理更通用的整数集，而无需对 IntSet 的用户进行修改。

对于包含 compute_at 的 schedules而言，InferBound 更为复杂。因此首先针对不包含 compute_at 的 schedules解读InferBound。

阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet

/*
 * 输入: Map<IterVar, Range> rmap: 包含 consumer stage 的每个 IterVar 的 Range
 * 输出: Map<IterVar, IntSet> up_state: 包含 consumer 的每个 leaf_iter_var 的 IntSet
 */

在阶段 1，根据 rmap 中 leaf_iter_vars 的 Range 创建每个 consumer 的 leaf_iter_vars 的 IntSet。consumer 已经被 InferBound 访问过，所以它所有的 IterVar 都知道 rmap 中的 Range。

有以下三种案例：

案例 1：leaf var 的 Range 范围为 1。这种情况下，leaf 的 up_state 只是一个点，等于 Range 的最小值。
案例 2：不需要释放。这种情况下，leaf 的 up_state 只是一个点，由 leaf var 本身定义。
案例 3：需要释放。这种情况下，leaf 的 Range 被简单地转换为 IntSet。

简单起见，假设 schedule 不包含线程轴。这种情况下，仅当 schedule 包含 compute_at 时，才和案例 2 相关。参阅 InferBound 与 compute_at 节来进一步获取更多信息。

阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root

/*
 * Input: Map<IterVar, IntSet> up_state: consumer leaf -> IntSet
 * Output: Map<IterVar, IntSet> dom_map: consumer root -> IntSet
 */

阶段 2 的目的是将 IntSet 信息从 consumer 的 leaf_iter_vars 传到 consumer 的 root_iter_vars。阶段 2 的结果是另一个映射 dom_map，其中包含每个 consumer 的 root_iter_vars 的 IntSet。

阶段 2 首先调用 PassUpDomain，它访问 consumer stage 的 IterVarRelations。在 Split 关系的情况下，PassUpDomain 根据内部和外部 IntSet 设置父级 IterVar 的 up_state，如下所示：

案例 1：外部和内部 IterVar 的范围匹配它们的 up_state 域。在这种情况下，只需将父级的 Range 转换为 IntSet 即可设置父级的 up_state。
案例 2：否则，父级的 up_state 是相对于外部和内部的*up_state通过评估 outer*f + inner + rmap[parent]->min 来定义的。这里，TVM 没有使用s**plit 关系的因子，而是用* f = rmap[inner]->extent。

仅当 schedule 包含 compute_at 时才需要案例 2。参阅下面的 InferBound 与 compute_at 节，进一步了解。

在 PassUpDomain 完成向 consumer 的所有 IterVars 传到 up_state 后，将创建一个从 root_iter_vars 到 IntSet 的新映射。如果 schedule 不包含 compute_at，则 root_iter_var iv 的 IntSet 由以下代码创建：

dom_map[iv->var.get()] = IntSet::range(up_state.at(iv).cover_range(iv->dom));

注意，若 schedule 不包含 compute_at，则实际上不需要阶段 1-2。dom_map 可以直接从 rmap 中的已知 Range 构建。Range 只需要转换为 IntSet，不会丢失信息。

阶段 3：将 IntSet 传到 consumer 的输入张量

/*
 * Input: Map<IterVar, IntSet> dom_map: consumer root -> IntSet
 * Output: Map<Tensor, TensorDom> tmap: output tensor -> vector<vector<IntSet> >
 */

注意，consumer 的输入张量是 InferBound 正在处理的 stage 的输出张量。因此，通过建立有关 consumer 输入张量的信息，实际上也获得了有关 stage 输出张量的信息：consumer 需要计算这些张量的某些区域。然后可以将该信息传到 stage 的其余部分，最终在阶段 4 结束时获得 stage 的 root_iter_vars 的 Range。

阶段 3 的输出是 tmap，它是一个包含所有 stage 输出张量的映射。张量是多维的，具有许多不同的轴。对于每个输出张量，以及每个张量的轴，tmap 包含一个 IntSet 列表。列表中的每个 IntSet 都是来自不同 consumer 的请求。

阶段 3 是通过在 consumer 上调用 PropBoundToInputs 来完成的。PropBoundToInputs 将 IntSet 添加到 tmap 的列表中，用于 consumer 的所有输入张量。

PropBoundToInputs 的具体行为取决于 consumer 操作的类型：ComputeOp、TensorComputeOp、PlaceholderOp、ExternOp 等。TensorComputeOp 的每个张量输入都有一个区域，定义了操作所依赖的张量切片。对于每个输入张量 i 和维度 j，根据 Region 中的相应维度向 tmap 添加一个请求：

for (size_t j = 0; j < t.ndim(); ++j) {
     // i selects the Tensor t
     tmap[i][j].push_back(EvalSet(region[j], dom_map));
}

阶段 4：整合所有 consumer

/*
 * Input: Map<Tensor, TensorDom> tmap: output tensor -> vector<vector<IntSet> >
 * Output: Map<IterVar, Range> rmap: rmap is populated for all of the stage's root_iter_vars
 */

阶段 4 由 GatherBound 执行，其行为取决于 stage 的操作类型。此处只讨论 ComputeOp，TensorComputeOp 情况类似。

ComputeOp 只有一个输出张量，其轴与 ComputeOp 的轴变量一一对应。ComputeOp 的 root_iter_vars 包括这些轴变量，以及 reduce_axis 变量。若 root IterVar 是一个轴变量，它对应一个输出张量的轴。 GatherBound 将此类 root IterVar 的 Range 设置为张量相应轴的所有 IntSet 的并集（即所有 consumer 请求的并集）。如果 root IterVar 是一个 reduce_axis，它的 Range 只是设置为其默认值（即 IterVarNode 的 dom 成员）。

// 'output' 选择输出张量
// i 是维度
rmap[axis[i]] = arith::Union(tmap[output][i]).cover_range(axis[i]->dom);

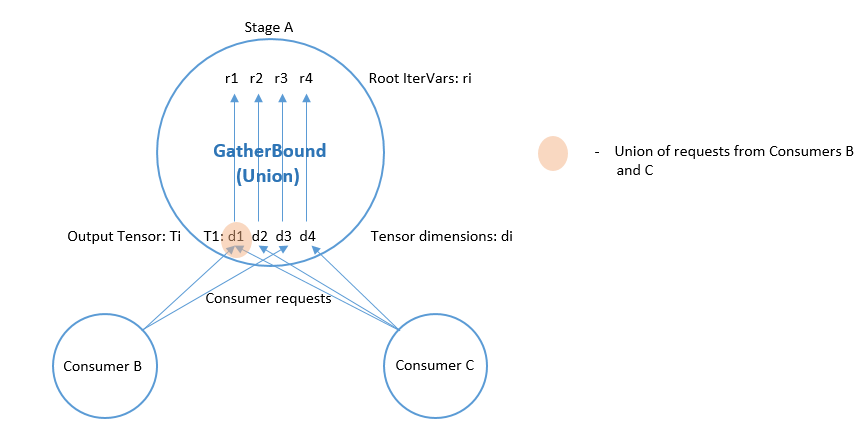
IntSet 的并集是通过将每个 IntSet 转换为一个区间来计算的，然后取所有最小值中的最小值，以及所有这些区间最大值中的最大值。

计算从未使用过的张量元素，显然会导致一些不必要的计算。

即使 IntervalSet 联合体不会产生非必要的计算，GatherBound 单独考虑张量的每个维度也会导致不必要的计算。例如，在下图中，两个 consumer A 和 B 需要 2D 张量的不相交区域：consumer A 需要 T[0:2, 0:2]，consumer B 需要 T[2:4, 2:4]。 GatherBound 分别对张量的每个维度进行操作。对于张量的第一维，GatherBound 采用区间 0:2 和 2:4 的并集，产生 0:4（注意，此处不需要近似值）。对于张量的第二维也是如此。因此，这两个请求的维度并集为 T[0:4, 0:4]。因此 GatherBound 将导致计算张量 T 的所有 16 个元素，即使这些元素中只有一半会被使用。

InferBound 与 compute_at

若 schedule 包含 compute_at，则 InferRootBound 的阶段 1-2 会变得更加复杂。

动机

例 1

考虑以下 TVM 程序片段：

C = tvm.compute((5, 16), lambda i, j : tvm.const(5, "int32"), name='C')
D = tvm.compute((5, 16), lambda i, j : C[i, j]*2, name='D')

会产生以下结果（简化的 IR）：

for i 0, 5
    for j 0, 16
        C[i, j] = 5
for i 0, 5
    for j 0, 16
        D[i, j] = C[i, j]*2

可以看出，stage D 需要计算 C 的所有（5,16）元素。

例 2

然而，假设 C 在 D 的轴 j 处计算：

s = tvm.create_schedule(D.op)
s[C].compute_at(s[D], D.op.axis[1])

那么一次只需要一个 C 元素：

for i 0, 5
    for j 0, 16
        C[0] = 5
        D[i, j] = C[0]*2

例 3

类似地，如果在 D 的 i 轴计算 C，则一次只需要一个包含 C 的 16 个元素的向量：

for i 0, 5
    for j 0, 16
        C[j] = 5
    for j 0, 16
        D[i, j] = C[j]*2

基于上述示例，很明显，InferBound 应该为 stage C 给出不同的答案，具体取决于它在其 consumer D 中「附加」的位置。

附加路径

若 stage C 在 stage D 的 j 轴上计算，我们说 C 附加到 stage D 的轴 j。这通过设置以下三个成员变量反映在 Stage 对象中：

class StageNode : public Node {
public:
    // 省略
    // 对于compute_at，attach_type = kScope
    AttachType attach_type;

    // 对于 compute_at，这是轴
    // 传递给 compute_at，例如 D.op.axis[1]
    IterVar attach_ivar;

    // 传递给 compute_at 的阶段，例如 D
    Stage attach_stage;

    // 省略
};

再次考虑上面的例子。为了让 InferBound 确定必须计算 C 的多少元素，重要的是，要知道 C 的计算是发生在 D 的叶变量的范围内，还是在该范围之上。在例 1 中，C 的计算发生在 D 的所有叶变量的范围之上。在例 2，C 的计算发生在 D 的所有叶变量的范围内。在例 3，C 出现在D 的 i 维度的范围内，但在 D 的 j 维度的范围之上。

CreateAttachPath 负责确定哪些作用域包含 stage C。这些作用域按从最内层到最外层的顺序排列。因此，对于每个 stage，CreateAttachPath 都会生成一个「附加路径」，其中列出了包含该 stage 从最里面到最外面的范围，在例 1，C 的附加路径为空。在例 2，C 的附加路径包含 {j，i}。在例 3，C 的附加路径是 {i}。

以下示例阐明了附加路径的概念，适用于更复杂的情况。

例 4

C = tvm.compute((5, 16), lambda i, j : tvm.const(5, "int32"), name='C')
D = tvm.compute((4, 5, 16), lambda di, dj, dk : C[dj, dk]*2, name='D')
s = tvm.create_schedule(D.op)
s[C].compute_at(s[D], D.op.axis[2])

这是 ScheduleOps 之后的 IR（注意，使用 ScheduleOps 的 debug_keep_trivial_loop 参数保留了范围为 1 的循环）：

realize D([0, 4], [0, 5], [0, 16]) {
  produce D {
    for (di, 0, 4) {
      for (dj, 0, 5) {
        for (dk, 0, 16) {
          realize C([dj, 1], [dk, 1]) {
            produce C {
              for (i, 0, 1) {
                for (j, 0, 1) {
                  C((i + dj), (j + dk)) =5
                }
              }
            }
            D(di, dj, dk) =(C(dj, dk)*2)
          }
        }
      }
    }
  }
}

在这种情况下，C 的附加路径是 {dk, dj, di}。注意 C 没有使用 di，但 di 仍然出现在 C 的附加路径中。

例 5

根据上述定义，可以很自然地在拆分后应用 Compute_at。下面例子中，C 的附着点是 D 的 j_inner。C 的附着路径是 {j_inner, j_outer, i}。

C = tvm.compute((5, 16), lambda i, j : tvm.const(5, "int32"), name='C')
D = tvm.compute((5, 16), lambda i, j : C[i, j]*2, name='D')
s = tvm.create_schedule(D.op)
d_o, d_i = s[D].split(D.op.axis[1], factor=8)
s[C].compute_at(s[D], d_i)

这个案例的 IR 如下所示：

for i 0, 5
    for j_outer 0, 2
        for j_inner 0, 8
            C[0] = 5
            D[i, j_outer*8 + j_inner] = C[0]*2

构建附加路径

继续参考上一节中介绍的 stage C 和 D。CreateAttachPath 算法按照如下方式构建 stage C 的附加路径。若 C 没有 attach_type kScope，则 C 没有附加内容，C 的附加路径为空；否则，在 attach_stage=D 处附加 C。

以自上而下的顺序遍历 D 的 leaf 变量。所有从 C.attach_ivar 或是更低位置开始的 leaf 变量都添加到 C 的附加路径中。然后，若 D 也附加到某个地方，例如 stage E ，则对 E 的 leaf 重复该过程。因此 CreateAttachPath 继续向 C 的附加路径添加变量，直到遇到没有附加的 stage。

在下面的示例中，C 附加到 D，D 附加到 E。

C = tvm.compute((5, 16), lambda ci, cj : tvm.const(5, "int32"), name='C')
D = tvm.compute((5, 16), lambda di, dj : C[di, dj]*2, name='D')
E = tvm.compute((5, 16), lambda ei, ej : D[ei, ej]*4, name='E')
s = tvm.create_schedule(E.op)
s[C].compute_at(s[D], D.op.axis[1])
s[D].compute_at(s[E], E.op.axis[1])

当 debug_keep_trivial_loop=True 时，C 的附加路径为 {dj,di,ej,ei}，D 的附加路径为 {ej,ei}：

// attr [D] storage_scope = "global"
allocate D[int32 * 1]
// attr [C] storage_scope = "global"
allocate C[int32 * 1]
produce E {
  for (ei, 0, 5) {
    for (ej, 0, 16) {
      produce D {
        for (di, 0, 1) {
          for (dj, 0, 1) {
            produce C {
              for (ci, 0, 1) {
                for (cj, 0, 1) {
                  C[(ci + cj)] = 5
                }
              }
            }
            D[(di + dj)] = (C[(di + dj)]*2)
          }
        }
      }
      E[((ei*16) + ej)] = (D[0]*4)
    }
  }
}

InferBound 与 compute_at

前面已经介绍了附加路径的概念，现在来看，若 schedule 包含 compute_at 时，InferBound 的不同之处。唯一的区别在于 InferRootBound，阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet 和阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root。

在 InferRootBound 中，目标是确定特定 stage C 的 root_iter_vars 的 Range。InferRootBound 的阶段 1-2 将 IntSet 分配给 C consumer 的 leaf IterVar，然后将这些 IntSet 传到 consumer 的 root_iter_vars。

若没有附加，则已经为 consumer 变量计算的 Range 定义了 consumer 需要多少 C。但是，若 stage 实际上在 consumer 变量 j 的一个范围内，那么一次只需要 j 的范围内的一个点。

阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet

/*
 * 输入：Map<IterVar, Range> rmap: contains the Range for each IterVar of the consumer stage
 * 输出：Map<IterVar, IntSet> up_state: contains an IntSet for each leaf_iter_var of the consumer
 */

阶段 1，根据 rmap 中的 leaf_iter_vars 的 Range 创建每个 consumer 的 leaf_iter_vars 的 IntSet。consumer 已经被 InferBound 访问过，所以它的所有 IterVar 都知道 rmap 中的 Range。

有以下三种案例：

案例 1：leaf var 的 Range 范围为 1。这种情况下，leaf 的 up_state 只是一个点，等于 Range 的最小值。
案例 2：不需要释放。这种情况下，leaf 的 up_state 只是一个点，由 leaf var 本身定义。
案例 3：需要释放。这种情况下，leaf 的 Range 被简单地转换为 IntSet。若在 consumer 中遇到 stage C 的附着点，就会发生案例 2。对于此 attach_ivar，以及 consumer 的所有更高叶变量，将应用案例 2。若 C 在叶变量的 Range 内，这将确保仅请求叶变量范围内的单个点。

阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root

/*
 * Input: Map<IterVar, IntSet> up_state: consumer leaf -> IntSet
 * Output: Map<IterVar, IntSet> dom_map: consumer root -> IntSet
 */

案例 1：外部和内部 IterVar 的 Range 匹配它们的 up_state 域。在这种情况下，只需将父级的 Range 转换为 IntSet 即可设置父级的 up_state。
案例 2：否则，父级的 up_state 是通过评估 outer*f + inner + rmap[parent]->min 来定义的，相对于外部和内部的 up_state。在这里，TVM 没有使用 split 关系的因子，而是使用* f = rmap[inner]->extent。

由于 schedule 包含 compute_at，因此可以应用案例 2。这是因为 leaf IntSet 现在可能会被初始化为其 Range 内的单个点（阶段 1 的案例 2：为 consumer 的 leaf_iter_vars 初始化 IntSet），因此 IntSet 无法总是与 Range 匹配。

PassUpDomain 将 up_state 向 consumer 传给所有 IterVars 后，将创建一个从 root_iter_vars 到 IntSet 的新映射。若 stage 没有附加到当前 consumer，那么对于 consumer 的 attach_path 中的每个变量 iv，将 iv 的 Range 添加到一个 relax_set。stage 的 root 变量是根据这个 relax_set 进行评估的。

这是为了处理类似以下示例的情况，其中 C 没有附加到任何地方，但它的 consumer D 在 stage E 中附加。这种情况下，在确定 C 有多少需要计算时，必须考虑 D 的 attach_path，{ej，ei}。

C = tvm.compute((5, 16), lambda ci, cj : tvm.const(5, "int32"), name='C')
D = tvm.compute((5, 16), lambda di, dj : C[di, dj]*2, name='D')
E = tvm.compute((5, 16), lambda ei, ej : D[ei, ej]*4, name='E')
s = tvm.create_schedule(E.op)
s[D].compute_at(s[E], E.op.axis[1])

for ci 0, 5
    for cj 0, 16
        C[ci, cj] = 5
for ei 0, 5
    for ej 0, 16
        D[0] = C[ei, ej]*2
        E[ei, ej] = D[0]*4

PassUpDomain 的限制

本节介绍 PassUpDomain 的已知限制。这些限制会影响 InferBound 生成的 Range，以及 PassUpDomain 的其他用户（例如 tensorize）。

例 6

上面仅讨论了 PassUpDomain 在 Split 关系上的行为。在以下示例中，schedule 除了 split 之外还包含 fuse。以下 TVM 程序中，operation C 有两个轴被融合，然后融合的轴被拆分。注意，所有张量最初的 shape 都是 (4, 4)，并且融合轴也被因子 4 分割。假设 fuse 的效果只是被 split 所抵消。然而，在 TVM 中并非如此，如下所述。

import tvm
from tvm import te

n = 4
m = 4

A = te.placeholder((n, m), name='A')
B = te.compute((n, m), lambda bi, bj: A[bi, bj]+2, name='B')
C = te.compute((n, m), lambda ci, cj: B[ci, cj]*3, name='C')

s = te.create_schedule(C.op)

fused_axes = s[C].fuse(C.op.axis[0], C.op.axis[1])
xo, xi = s[C].split(fused_axes, 4)

s[B].compute_at(s[C], xo)

print(tvm.lower(s, [A, C], simple_mode=True))

该程序的输出如下所示。注意，每次通过外循环计算 B 的所有 16 个元素，即使 C 只使用其中的 4 个。

// attr [B] storage_scope = "global"
allocate B[float32 * 16]
produce C {
  for (ci.cj.fused.outer, 0, 4) {
    produce B {
      for (bi, 0, 4) {
        for (bj, 0, 4) {
          B[((bi*4) + bj)] = (A[((bi*4) + bj)] + 2.000000f)
        }
      }
    }
    for (ci.cj.fused.inner, 0, 4) {
      C[((ci.cj.fused.outer*4) + ci.cj.fused.inner)] = (B[((ci.cj.fused.outer*4) + ci.cj.fused.inner)]*3.000000f)
    }
  }
}

这与下面的 IR 形成对比，后者是通过删除 fuse 和 split 修改上述程序，并将 compute_at 替换为 s[B].compute_at(s[C], C.op.axis[0]) ，注意，在下面的 IR 中，根据需要一次只计算 B 的 4 个元素。缓冲区 B 也更小。

// attr [B] storage_scope = "global"
allocate B[float32 * 4]
produce C {
  for (ci, 0, 4) {
    produce B {
      for (bj, 0, 4) {
        B[bj] = (A[((ci*4) + bj)] + 2.000000f)
      }
    }
    for (cj, 0, 4) {
      C[((ci*4) + cj)] = (B[cj]*3.000000f)
    }
  }
}

这个例子表明，与预期相反，split 并非只是抵消 fuse。那么造成这种差异的原因是什么？当一次实际上只需要一行时，为什么要重新计算整个张量 B 4 次？

InferBound 的任务是确定必须计算的 B 的数量。但是，在这种情况下，InferBound 为 B 的 root_iter_vars 返回的范围太大：对于 bi 和 bj 都是 [0, 4]。这是因为 PassUpDomain 对 Fuse 关系的限制，后续将进行详细解释。

当 InferRootBound 在 stage B 工作时，它会访问 B 的 consumer stage C，以了解 C 请求了多少 B。C 有 root_iter_vars ci 和 cj，已经融合并进行了分割。这导致了 stage C 的以下 IterVar Hyper-graph。

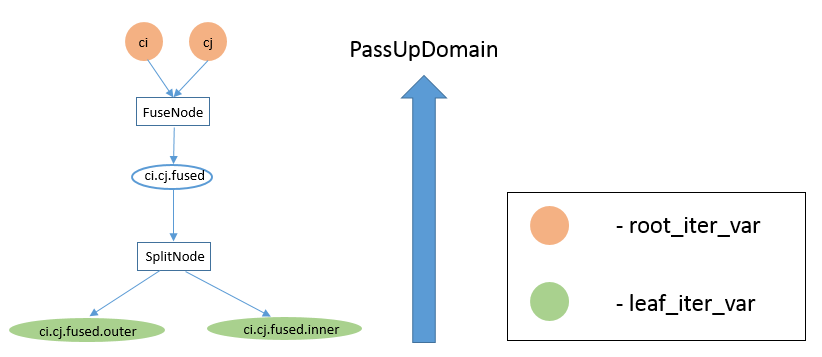
在 stage B 上跟踪 InferRootBound 的执行。阶段 1：为 InferRootBound 的 consumer leaf_iter_vars 初始化 IntSet 涉及为 B 的 consumer stage C 的所有 leaf_iter_vars 设置 IntSet。在这种情况下，C 的 leaf_iter_vars 是 ci.cj.fused.outer 和 ci.cj.fused.inner。由于 B 附加在 ci.cj.fused.outer 处，因此 ci.cj.fused.inner 必须释放，但 ci.cj.fused.outer 是单点。 C 的 leaf_iter_vars 的 IntSet，在阶段 1：为 consumer leaf_iter_vars 初始化 IntSet 之后，如下表所示。

IterVar	IntSetafter Phase 1
ci.cj.fused.inner	[0, (min(4, (16 - (ci.cj.fused.outer*4))) - 1)]
ci.cj.fused.outer	[ci.cj.fused.outer, ci.cj.fused.outer]

在 InferRootBound 的阶段 2：将 IntSet 从 consumer leaf 传到 consumer root 中，以自下而上的顺序在所有 C 的 IterVarRelations 上调用 PassUpDomain。

PassUpDomain 首先在 C 的 Split 节点上调用。PassUpDomain 的案例 2 适用，因为 ci.cj.fused.outer 的 IntSet 只是一个点，并且不等于它的 Range（如先前在 stage C 上由 InferBound 计算的那样）。因此，PassUpDomain 根据 ci.cj.fused.inner 和 ci.cj.fused.outer 的 IntSet 设置 ci.cj.fused 的 IntSet，如下表第 3 行所示。

IterVar	IntSetafter PassUpDomain on SplitNode
ci.cj.fused.inner	[0, (min(4, (16 - (ci.cj.fused.outer*4))) - 1)]
ci.cj.fused.outer	[ci.cj.fused.outer, ci.cj.fused.outer]
ci.cj.fused	[(ci.cj.fused.outer4), ((ci.cj.fused.outer4) + (min(4, (16 - (ci.cj.fused.outer*4))) - 1))]

在 Split 节点调用 PassUpDomain 后，在 Fuse 节点也进行调用。

案例 1：IterVarfused 的 Range（如先前由 InferBound 计算的那样）等于其 IntSet
案例2：IterVar fused 的 IntSet 是单点
案例3：其他情况

示例中，ci.cj.fused 的 Range 是 [0, 16)。不同于 ci.cj.fused 的 IntSet，其范围最多为 4（见上表第 3 行）。因此案例 1 不适用。案例 2 也不适用，因为 ci.cj.fused 的 IntSet 不是单点。因此，仅适用于默认案例 3。

在案例 3 中，PassUpDomain 保守地应用了「回退（fallback）推理规则」，即它只返回等于 ci 和 cj 的 Range 的 IntSet。由于 C 是 schedule 的输出 stage，InferBound 会将 C 的 root_iter_vars（即 ci 和 cj）的 Range 设置为它们的原始维度（即它们的 IterVars 的 dom 值）。ci 和 cj 的 PassUpDomain 的结果输出显示在下表的最后两行中。

IterVar	IntSetafter PassUpDomain on FuseNode
ci.cj.fused.inner	[0, (min(4, (16 - (ci.cj.fused.outer*4))) - 1)]
ci.cj.fused.outer	[ci.cj.fused.outer, ci.cj.fused.outer]
ci.cj.fused	[(ci.cj.fused.outer4), ((ci.cj.fused.outer4) + (min(4, (16 - (ci.cj.fused.outer*4))) - 1))]
ci	[0, 4]
cj	[0, 4]

这足以保证 consumer C 请求 B 的所有元素：ci 和 cj 的 IntSet 成为 consumer C 对 stage B 输出张量的请求（通过阶段 3：将 IntSet 传到 consumer 的输入张量中的 PropBoundToInputs 和阶段 4：整合所有 consumer 中的 GatherBound）。

此示例表明，包含融合轴拆分的 schedule 很难在 TVM 中处理。难度源自 GatherBound 的限制。consumer C 请求的张量 B 的区域必须是 B 的单个矩形区域。或者，若 B 有两个以上的维度，则 B 区域必须可表示为每个轴的独立 Range。

若 split 因子为 4 或 8，以上示例中，外循环每次迭代所需的 B 区域是矩形的。

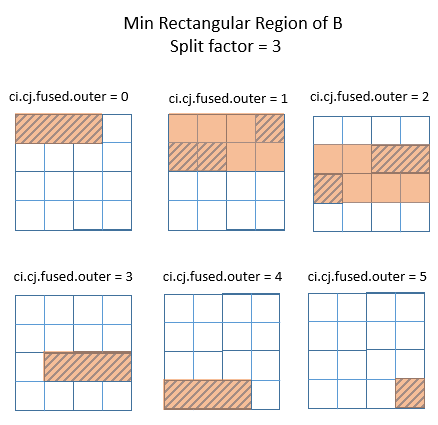
但是，若上例中的拆分因子从 4 变为 3，则很容易看出，C 所需要的 B 区域无法继续通过其每个轴的独立 Range 来描述了。

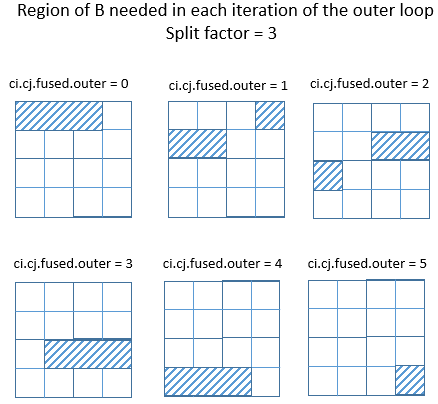
下图显示了矩形区域所能达到的最佳效果。橙色区域是在外循环的每次迭代中覆盖需要计算的 B 区域的最小矩形区域。

InferBound Pass

IterVar Hyper-graph​

PassDownDomain​

InferRootBound​

IntSet​

阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet​

阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root​

阶段 3：将 IntSet 传到 consumer 的输入张量​

阶段 4：整合所有 consumer​

InferBound 与 compute_at​

动机​

附加路径​

构建附加路径​

InferBound 与 compute_at​

阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet​

阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root​

PassUpDomain 的限制​

IterVar Hyper-graph

PassDownDomain

InferRootBound

IntSet

阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet

阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root

阶段 3：将 IntSet 传到 consumer 的输入张量

阶段 4：整合所有 consumer

InferBound 与 compute_at

动机

附加路径

构建附加路径

InferBound 与 compute_at

阶段 1：为 consumer 的 leaf_iter_vars 初始化 IntSet

阶段 2：将 IntSet 从 consumer 的 leaf 传到 consumer 的 root

PassUpDomain 的限制